“수학 역사상 가장 아름다운 우연”
두 세계는 절대 만나지 않을 줄 알았다.
타원곡선과 모듈러 형식.
하지만 이들의 연결이 ‘오작교’가 되었다.
타니야마-시무라 추측은 어떻게 페르마의 마지막 정리를 해결했을까?
앤드루 와일즈가 평생을 걸고 증명한 이 위대한 수학적 연결은
전혀 다른 두 수학 세계가 만나는 기적이었다.
페르마 정리, 타원곡선, 모듈러 형식, 그리고 와일즈의 드라마까지
한 편의 이야기처럼 소개한다.
목차
- 페르마의 마지막 정리란?
- 왜 아무도 이 정리를 못 풀었을까?
- 타원곡선이란 무엇인가?
- 모듈러 형식은 또 뭐지?
- 타니야마-시무라 추측: 두 세계를 잇는 다리
- 앤드루 와일즈, 평생의 꿈에 불을 지피다
- 결정적 순간: 페르마 정리의 몰락
- 이후의 이야기와 현대 수학에 미친 영향
- 정리하며: 왜 이 이야기를 기억해야 할까?
1. 페르마의 마지막 정리란?
수학자 피에르 드 페르마는 이렇게 적었다.
“세제곱 이상의 자연수에 대해 aⁿ + bⁿ = cⁿ을 만족하는 해는 존재하지 않는다.
나는 이 정리에 대한 놀라운 증명을 갖고 있지만 이 여백은 부족하다.”
이 말은 수세기 동안 수학자들을 괴롭혔다.
수학계의 전설이자 저주,
이 정리는 무려 350년간 아무도 풀지 못한 채 남아 있었다.
2. 왜 아무도 이 정리를 못 풀었을까?
왜냐하면 이 문제는 정수론 문제인데,
풀기 위해선 20세기 고급 대수기하학과 모듈러 형식 이론이 필요했기 때문.
당대 수학자들은 도저히 이 문제를 현대 수학 언어로 번역하지 못했다.
그게 가능해진 건, 전혀 다른 영역에 있던 두 수학 세계가 연결된 덕분이었다.
그 가설이 바로, 타니야마-시무라 추측이다.
3. 타원곡선이란 무엇인가?
타원곡선은 이렇게 생긴 함수다:
y² = x³ + ax + b
하지만 그냥 방정식이 아니다.
정수해, 유리수해를 다루는 정수론의 핵심 도구다.
암호학, 난수 생성, 블록체인 기술에도 활용될 만큼 중요하다.
특히, 어떤 타원곡선이 모듈러 형식이라는 존재와 연결될 수 있다면
엄청난 의미를 갖는다.

4. 모듈러 형식은 또 뭐지?
이건 완전히 다른 세계의 존재다.
함수인데, 정해진 대칭을 가지면서도 무한한 정보를 품고 있다.
다르게 말하면,
‘함수들의 우주’에서 특정한 패턴으로 자기복제와 변형을 허용하는 존재다.
모듈러 형식은 보통 해석학과 복소수의 세계에서 살고 있다.
그런데 문제는, 이 모듈러 형식과 타원곡선이 전혀 다르다는 점.

5. 타니야마-시무라 추측: 두 세계를 잇는 다리
1955년, 일본의 수학자 타니야마 유타카는
"모든 타원곡선은 어떤 모듈러 형식과 연결된다"는 충격적인 추측을 발표했다.
수학자들은 처음엔 믿지 않았다.
너무 말이 안 됐기 때문이다.
하지만 일부 곡선에 대해 실험 결과가 맞아떨어졌고,
시무라 고로가 이를 정리하면서 ‘타니야마-시무라 추측’으로 불리게 됐다.
이 추측은 곧 와일즈라는 소년의 마음에 로맨스의 불을 지핀다.

6. 앤드루 와일즈, 평생의 꿈에 불을 지피다
10살의 와일즈는 도서관에서 페르마의 정리를 처음 만난다.
그리고 결심한다. “내가 이걸 풀 거야.”
그는 자라면서 이 문제에 필요한 모든 수학을 익혔다.
그리고 1986년, 타니야마-시무라 추측이 맞다면,
페르마의 마지막 정리도 자동으로 맞다는 연결고리가 발견된다. (프레이 곡선 + 리벳의 아이디어)
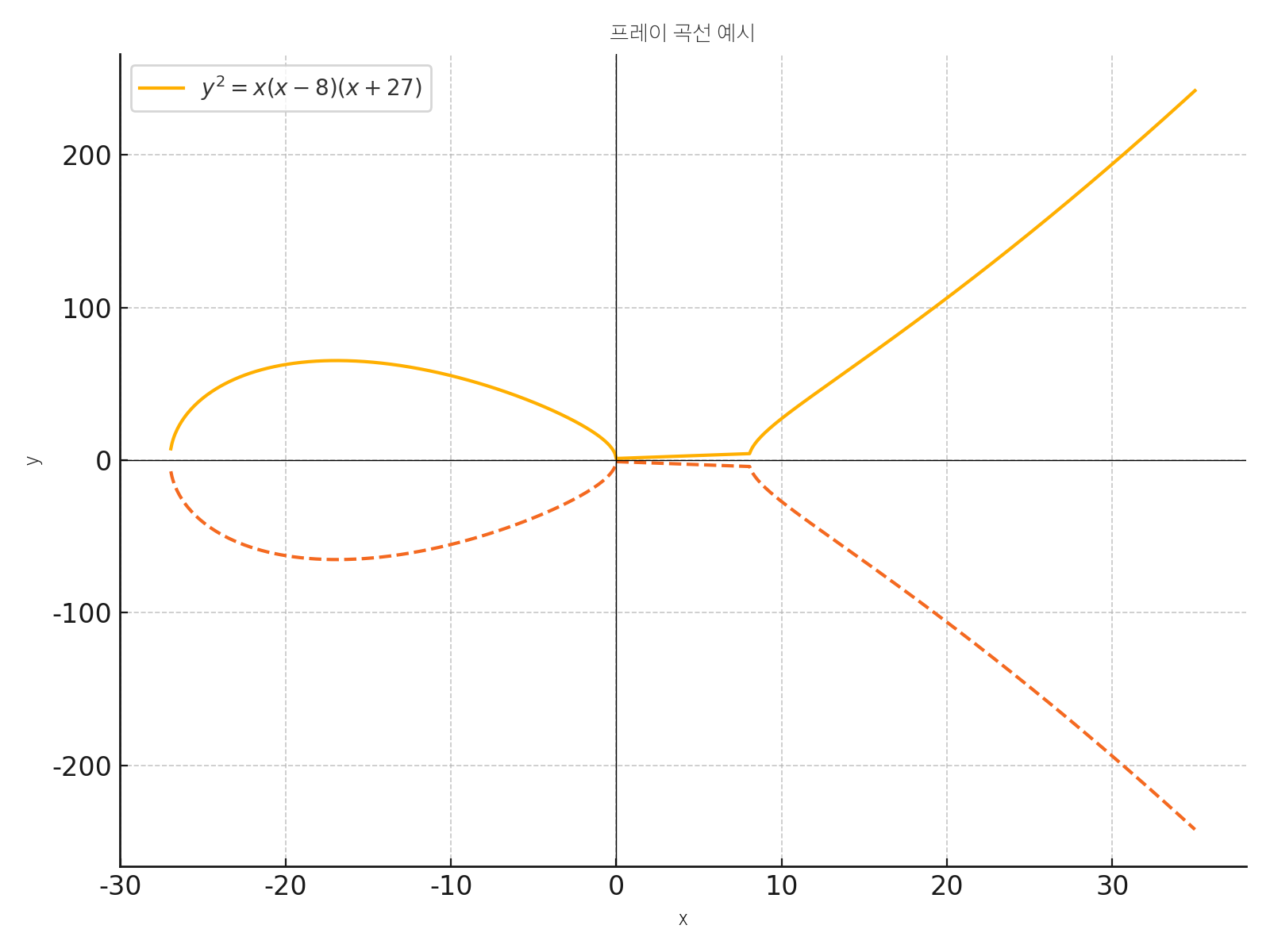
와일즈는 이를 본 순간, 운명이 왔다고 느낀다.
자신이 평생 쌓아온 모든 수학이 이 순간을 위한 것처럼.
7. 결정적 순간: 페르마 정리의 몰락
와일즈는 7년간 아무에게도 말하지 않고 혼자서 연구했다.
1993년, 케임브리지에서 발표.
하지만... 오류 발견.
무너지는 듯했지만, 조수 리처드 테일러와 함께 1년간 수정한 끝에
1994년, 마침내 증명에 성공한다.
페르마의 마지막 정리는
타니야마-시무라 추측의 특별한 경우로 증명된 것이다.
8. 이후의 이야기와 현대 수학에 미친 영향
타니야마-시무라 추측은 이후 ‘모듈러성 정리(Modularity Theorem)’로 불리며
수많은 응용과 연구를 이끌었다.
이 추측은 지금도 수학의 여러 분야에서 핵심 이론으로 작동하고 있다.
그리고 와일즈는 이 공로로
수학계의 노벨상이라 불리는 ‘아벨상’을 수상했다.
9. 정리하며: 왜 이 이야기를 기억해야 할까?
타니야마-시무라 추측과 페르마 정리의 연결은
그 자체로도 아름답지만,
수학이 어떻게 서로 다른 영역을 하나로 연결하면서 확장되는지를 보여주는 최고의 사례다.
불가능해 보이던 연결,
집요한 추적,
그리고 평생의 헌신이 만들어낸 기적.
앤드루 와일즈가 말했다.
“이건 내 인생의 순간이었고, 그 순간은 영원히 나만의 것이다.”

© 콘텐츠 훈련소 - 수학픽(Math Pick)
(무단 복제 및 재배포를 금합니다. 인용 시 출처 표기 바랍니다.)
'바로 써먹는 수학픽' 카테고리의 다른 글
| 실명한 수학자, 열세 자녀의 아버지, 그리고 800편의 논문 – 오일러 이야기 (0) | 2025.04.21 |
|---|---|
| 프레이 곡선과 리벳의 아이디어: 페르마 정리의 숨겨진 연결고리 (1) | 2025.04.20 |
| 🔢 소수를 쫓는 사람들 Ep.10 <소수의 끝, 무한의 시작 – 지금 우리가 던져야 할 질문> (0) | 2025.04.10 |
| 🔢 소수를 쫓는 사람들 Ep.09 <하디 & 리틀우드 – 수학의 우정이 쓴 정밀한 예언> (0) | 2025.04.10 |
| 🔢 소수를 쫓는 사람들 Ep.08 <리만 – 소수의 심연을 들여다본 자> (0) | 2025.04.10 |

