13명의 자녀를 둔 아버지이자, 실명 후에도 연구를 멈추지 않았던 천재 수학자 오일러. π, i, e를 하나로 묶어낸 수식처럼, 그는 서로 다른 개념을 통합하는 창의융합형 인재였다. 지금 우리 시대가 원하는 인간상이란 무엇인가? 오일러의 삶을 통해 들여다본다.
📌 목차
- 오일러, 수학을 품은 아버지
- 수학을 사랑한 사람
- ‘다른 것’을 연결하는 능력자
- 기호를 만든 창조자
- 어떻게 그런 사람이 될 수 있었을까?
- 죽음마저도 수학과 함께
- 콘텐츠 훈련소가 꿈꾸는 인간상
- 관련 키워드 & 마무리
1. 오일러, 수학을 품은 아버지
애를 얼르면서 논문을 쓴 수학자.
표면적으로는 전혀 상관없는 아이디어들을 서로 엮는 데 탁월했던 ‘연결의 천재’.
바로 레온하르트 오일러(Leonhard Euler) 이야기다.
그는 원의 둘레와만 관련 있어 보이는 π를 가지고, 수학사상 가장 아름답다는 다음 공식을 만들었다.
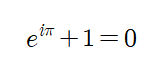
그리고 13명의 자녀를 둔 아버지이자, 실명 후에도 연구를 멈추지 않았던 천재 수학자였다.
2. 수학을 사랑한 사람
오일러는 수학을 ‘공부’한 사람이 아니다. 수학으로 호흡한 사람이다.
그에게 수학은 삶이었고, 사유였고, 표현이었다.
- 하루에 12시간 이상 계산하는 일이 흔했고
- 아내와 아이들이 곁에 있어도 집중은 흐트러지지 않았으며
- 심지어 양쪽 시력을 모두 잃은 뒤에도,
350편 이상의 논문을 구술로 발표했다.
그는 말 그대로 ‘보이지 않아도 보았던 사람’이다.
3. ‘다른 것’을 연결하는 능력자
오일러의 위대함은 단순한 계산 능력에 있지 않다.
그는 관련 없어 보이는 것들을 하나의 구조로 묶어내는 데 천재였다.
- 삼각함수와 복소수의 결합 이 수식 하나로 파동, 전자기, 양자역학의 기초가 열렸다.
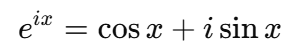
- 수학 5대 상수의 통합 수학의 세계관이 응축된 공식. e, π, i, 1, 0 — 이질적인 개념이 하나로 연결된 순간이었다.

복잡한 것을 단순하게,
멀리 있는 것을 가까이 묶는 것.
그게 오일러의 수학이었다.
4. 기호를 만든 창조자
우리가 오늘날 사용하는 수학 기호 중 많은 것들이 오일러의 손에서 나왔다.
- 함수 표기 f(x)
- 자연로그의 밑 e
- 허수 단위 i
- 삼각함수 sin, cos, tan
- 합을 나타내는 기호 Σ
오일러는 단지 계산하는 사람이 아니었다.
수학을 언어로 바꾸고, 개념을 기호로 부호화한 설계자였다.
기호는 단순한 약속이 아니라,
사고를 구조화하는 도구다.
5. 어떻게 그런 사람이 될 수 있었을까?
오일러는 어린 시절부터 인문과 자연과학을 모두 익혔다.
신학, 철학, 언어, 고전, 그리고 음악까지 그의 사유는 입체적이었다.
그의 특징은 이렇다:
- 글을 잘 썼다 – 누구보다 논리적이었고, 설명이 뛰어났다.
- 타인과 토론하며 생각을 확장했다.
- 몰입력이 강해, 주변 소음에도 집중이 흐트러지지 않았다.
- 개념을 구조화하고 연결하는 힘이 탁월했다.
이 모든 요소가 오일러를 융합형 인재, 창의적 설계자로 만들었다.
6. 죽음마저도 수학과 함께
오일러는 생애 마지막 날에도 계산을 했다.
그날 저녁, 그는 이렇게 말했다고 전해진다.
“오늘은 정말 멋진 계산을 했군.”
그리고 곧 세상을 떠났다.
수학을 사랑한 사람의 마지막 인사였다.
7. 콘텐츠 훈련소가 꿈꾸는 인간상
콘텐츠 훈련소는 오일러 같은 사람을 지향한다.
단지 많이 아는 사람을 원하지 않는다.
우리가 함께 만들고 싶은 인재는,
- 깊이 생각하고
- 다양한 분야를 연결하며
- 자기만의 언어로 표현할 줄 아는 사람
- 그리고 몰입의 기쁨을 아는 사람
그 모든 가능성을 오일러는 이미 보여주었다.

© 콘텐츠 훈련소 [콘텐츠 마스터]
'바로 써먹는 수학픽' 카테고리의 다른 글
| e는 무리수다. 그런데 초월수라고도 한다? (0) | 2025.04.22 |
|---|---|
| 자연상수 e를 수학의 중심으로 끌어올린 오일러, 그리고 e와 π가 만나는 순간 (0) | 2025.04.22 |
| 프레이 곡선과 리벳의 아이디어: 페르마 정리의 숨겨진 연결고리 (1) | 2025.04.20 |
| 타니야마-시무라 추측: "페르마의 마지막 정리"와 수학자들의 마지막 로맨스 (0) | 2025.04.20 |
| 🔢 소수를 쫓는 사람들 Ep.10 <소수의 끝, 무한의 시작 – 지금 우리가 던져야 할 질문> (0) | 2025.04.10 |



