라디안(radian)은 분명 '각도 단위'인데,
왜 정의는 '길이 ÷ 반지름'일까요?
처음 수학에서 라디안을 배우면 누구나 한 번쯤 의문을 가집니다.
“라디안은 각도인데, 왜 자꾸 길이로 말하지?”
이번 글에서는 이 헷갈림을 완전히 정리해드릴게요.
✅ 라디안의 정의부터 다시 살펴보자
먼저 라디안의 수학적 정의는 이렇습니다.
라디안은 호의 길이를 반지름으로 나눈 비율이다.
공식으로 표현하면 다음과 같습니다:
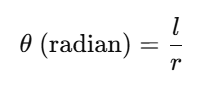
- : 호의 길이 (길이 단위, m 또는 cm 등)
- : 반지름 (역시 길이 단위)
- θ : 중심각 (단위는 '라디안')
즉, 라디안은 길이 ÷ 길이 = 단위 없는 수,
그런데 이 ‘단위 없는 비율’을 각도 단위로 약속한 것이 바로 라디안입니다.
🤔 그런데 이게 왜 각도를 나타낼 수 있지?
한 번 그림으로 상상해 보세요.
- 반지름이 1인 원이 있고,
- 원 위에서 호의 길이 이 되는 지점을 연결해서 만든 중심각이 있다고 해요.
이때 이 중심각을 1라디안이라고 부릅니다.
🌟 핵심 아이디어
‘반지름과 같은 길이의 호’를 가진 중심각이 1라디안이다.
즉, 라디안은 '각의 크기'를 거리 기준으로 정의한 단위예요.
🌀 원 전체는 몇 라디안일까?
원 전체의 둘레는?

이 둘레 전체를 반지름 r로 나누면?

즉, 한 바퀴를 돌았을 때의 중심각의 크기가 2π 라디안이라는 뜻입니다.
우리가 흔히 쓰는 360도가 수학적으로는 라디안인 거죠.

📏 다시 말해, 라디안은 왜 ‘길이’로 설명될까?
정확히 말하면, 라디안 자체가 길이는 아니에요.
다만, 라디안은 길이와 길이의 비율로 정의된 각도 단위입니다.

반지름으로 나눈 호의 길이가 바로 중심각이 되는 것이고,
그걸 ‘라디안’이라는 이름의 각 단위로 쓰자고 정의한 거예요.
📚 요약 정리
- 라디안은 각도를 재는 단위이지만, 정의는 비율입니다.
- 라디안은 각을 자연스럽고 수학적으로 정의하는 방식입니다.
- 단위가 없어 보이지만, '각의 크기'를 직접 계산할 수 있는 유용한 방식입니다.
🔍 덧붙이는 이야기: 왜 라디안을 쓸까?
미적분, 삼각함수에서 각도를 라디안으로 써야만 자연스럽게 미분이 잘 돼요.
예를 들어:

이건 x가 라디안일 때만 성립합니다.
도 단위로 쓰면 이상한 보정 계수가 생겨요.
🎯 그래서 고급 수학에서는 항상 라디안 단위를 씁니다.
✏️ 마무리하며
라디안은 ‘길이’가 아니라, 길이를 이용해 정의한 '각도 단위'입니다.
수학적으로 훨씬 자연스럽고, 물리학, 공학, 미적분에서도 반드시 쓰는 이유가 여기에 있어요.
“길이로 정의한 각도”라는 발상의 전환,
이게 라디안의 진짜 매력입니다.
🎯 왜 파이(3.14...)가 180도일까? (1탄)수학을 좋아하든 말든, 이건 누구나 궁금한 이야기
🤔 3.14가 왜 각도를 뜻하지?수학을 싫어하는 사람도 ‘파이’는 안다.3.14, 원주율, 원둘레 공식, 뭔가 복잡한 수학 시험의 트라우마...그런데 어느 날 문득, 누군가 이렇게 물었다.“왜 180도가 π
studygoodjob.com
왜 파이(3.14...)가 180도일까? (3탄)-라디안은 단위가 없다? 그런데 왜 "1라디안"이라고 부를까?
“라디안은 각도의 단위입니다.”하지만 자세히 들여다보면, 라디안은 사실 단위가 없는 수입니다.그런데도 우리는 흔히 “1라디안”이라는 표현을 씁니다.도대체 단위가 없다면서 왜 단위처
studygoodjob.com
'바로 써먹는 수학픽' 카테고리의 다른 글
| 기울기는 단위가 뭐예요? 기울기에 대한 진짜 궁금한 점 (0) | 2025.05.15 |
|---|---|
| 왜 파이(3.14...)가 180도일까? (3탄)-라디안은 단위가 없다? 그런데 왜 "1라디안"이라고 부를까? (0) | 2025.05.15 |
| 🧮중1 수학 1단원 공식 정리: 수와 연산 (시험 전에 볼 것 정리) (1) | 2025.05.15 |
| 📘 [생활 속의 수학 ④] 물고기 잡힐 확률은?– 조건부 확률과 낚시 전략 (0) | 2025.05.07 |
| 📘 [생활 속의 수학 ⑤] 낚시 포인트는 어떻게 찾을까?– 삼각법과 좌표의 수학 (0) | 2025.05.07 |



